Opened 17 years ago
Last modified 17 years ago
#664 closed enhancement
Preconditioned simulation of BSR linear block — at Initial Version
| Reported by: | Víctor de Buen Remiro | Owned by: | Víctor de Buen Remiro |
|---|---|---|---|
| Priority: | highest | Milestone: | Numerical methods |
| Component: | Math | Version: | 2.0.1 |
| Severity: | major | Keywords: | BSR, linear, ARIMA, preconditioned |
| Cc: |
Description
In each iteration of BSR, we need to simulate vector 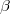 matching this linear regression with ARIMA noise:
matching this linear regression with ARIMA noise:
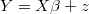
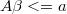
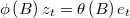
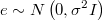
ARMA and variance parameters are changing in each iteration of BSR, and, if there are missing values or non linear filters matrices 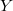 and
and 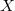 could also change in each iteration. So, an ARIMA decomposition and filter and a Cholesky decomposition is needed in order to simulate linear block. Even if
could also change in each iteration. So, an ARIMA decomposition and filter and a Cholesky decomposition is needed in order to simulate linear block. Even if 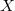 is very sparse, after applying ARIMA filter it could become dense and process will be too slow.
is very sparse, after applying ARIMA filter it could become dense and process will be too slow.
I propose a preconditioning method to save a lot of time calculating and storing all blocks of a simulation only for one of K iterations and using them to generate aproximations that will be refinated in this fast way.
Let be the last full calculated and stored system
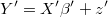
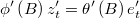
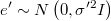
- Since this system has been previously decomposed is very fast to generate a vector
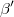 matching it
matching it
- The corresponding ARIMA noise is simply
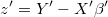
- By means of Almagro method it's posible to calculate residuals
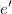 and initial values
and initial values 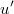 that solve difference equation
that solve difference equation
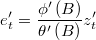
- Then we can purpose residuals and initial values for current system as
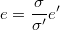
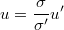
- ARIMA noise for current system becomwes simply
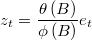
- Then, we can solve sparse linear system
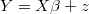
- El vector resultante se aceptará si se cumplen las restricciones
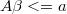
y de lo contrario se repite el proceso entero.
Cuando el número de repeticiones se hace insoportable se debe reemplazar el sistema almacenado.
